ELECTRICITÉ
Chapitre 1: Bases de l'électrocinétique
I - Généralités
sur les circuits électriques:
Dipôle
électrique:
Système
électrique relié à
l'extérieur par deux bornes: 
Réseau
électrique:
Système de
dipôles
reliés par des conducteurs filiformes de
résistance
négligeable.
Nœud: Point relié
par des fils à plus de deux dipôles.
Branche: Portion du
réseau comprise entre deux nœuds voisins.
Maille: Parcours
fermé constitué de branches et ne passant qu'une
fois par un nœud donné.
Graphe: Schéma
représentatif de la topologie du réseau (nature
des interconnections) indépendamment de sa forme
réelle.
-Exemple de
différents graphes pour un même réseau:
nœuds: A, B, C
et D (n=4)
branches: AD, DC, DB,
BC, AB et AC (b=6)
mailles
indépendantes (qui ne sont pas elle-mêmes
constituées d'autres mailles):
ABCA (en passant par E et F), ADBA et DCBD (m=3)
remarques:
-Le
graphe 1
présente un
chevauchement, un graphe est plus facile à analyser lorqu'il
est
mit à plat comme pour G2 et G3.
-ADCB, par exemple, est une maille non indépendante.
pour information, on montre
que: m = b - n + 1 .
L'état
physique du réseau est connu quand on a
déterminé les courants et les tensions de
chacunes des
branches (état macroscopique).
Au niveau
microscopique, il y a des porteurs de charges dans les
conducteurs qui sous l'action d'un champ électrique
extérieur se déplacent. Pour un métal
ce sont des
électrons qui se déplacent au sein du
réseau
cristallin du métal. Pour les électrolytes les
ions
jouent le rôle de charge libre.
Charge
élémentaire: e  1,6.10-19
C
(C:
Coulomb), pour un électron q=-e.
1,6.10-19
C
(C:
Coulomb), pour un électron q=-e.
II
- Grandeurs
électriques
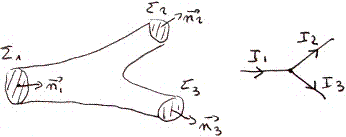
1) Intensité
a) Définition: |
 |
Cette
convention permet de faire abstraction du signe des charges
transportée: par exemple dans une électrolyse
interviennent des cations, des anions et des électrons, mais
une
même quantité d'électricité
est
transporté.
|

I
est une quantité algébrique. |
b) Loi
des nœuds:
En régime
permanent il n'y a pas d'accumulation de charges et il y a conservation
de la charge électrique:
Pendant  t: t:  Q1
= Q1
=  Q2
+ Q2
+  Q3 Q3
  Q1/ Q1/ t = t =  Q2/ Q2/ t + t +  Q3/ Q3/ t t  quand quand  t tend vers
zéro : t tend vers
zéro :
I1
= I2
+ I3 .
|
 |
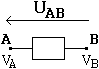
2) Tension:
a) Définition:
Si nous imposons un potentiel électrique
différent en deux point d'un circuit un champ
électrique est créé et les charges se
mettent en mouvement. Soient VA et VB
les potentiels en deux points d'un circuit, alors on défini
la tension entre les points A et B comme une différence de
potentiels:
UAB
= VA - VB
flêche
de B vers A
U est
une quantité algébrique. |
 |
3)
L'approximation des régimes quasi-pemanents (ARQP)
Les lois
des nœuds
et des mailles ne peuvent pas s'appliquer à toutes les
situations. Vous montrerez l'année prochaine qu' il est
nécessaire que les courants et le tensions du
réseau
soient continus ou "lentement" variables. Si d est la taille du circuit
et  la
longueur d'onde électromagnétique du
problème
alors pour réaliser l'approximation on doit avoir d
très
petit devant
la
longueur d'onde électromagnétique du
problème
alors pour réaliser l'approximation on doit avoir d
très
petit devant  :
d<<
:
d<<
Nous avons  =c/f, avec c la vitesse
de la lumière dans le vide et f la
fréquence de l'onde.
=c/f, avec c la vitesse
de la lumière dans le vide et f la
fréquence de l'onde.
f
|
50
Hz |
1
MHz |
100
MHz |
10
GHz |
 |
6000
km |
300
m |
3
m |
3
cm |
Dans une
installation domestique sous 50 Hz l'ARQP s'applique
aisément, mais pas pour l'antenne de votre radio!
III - Dipôles
électriques:
1) Convention
générateurs et récepteurs
Pour un
dipôle AB les choix d'orientations de la tension et
du courant sont indépendants et arbitraires, mais, le choix
fait, il est crucial de bien noter les sens relatifs choisis:
On dit que le
dipôle est étudié en convention
récepteur
lorsque U et I sont
orientés en sens contraire.
On dit que le
dipôle est étudié en convention
générateur
lorsque U et I sont
orientés dans le même sens.
D'où
quatre possibilités pour un dipôle:

En convention
récepteur :
P = U I
(CR)
En convention
générateur :
P = - U I
(CG)
La puissance
s'exprime en Watt, et correspond à
l'énergie reçue par unité de temps.
C'est une puissance instantanée qui mesure
l'énergie reçue par le dipôle par
unité de temps via le reste du circuit: P = Préseaux
-> dipôle
= - Pdipôle-> réseaux
. Cette puissance est reçue
par le dipôle et donc fournie
par le reste du cicuit.
3) Caractéristique
d'un dipôle
La
caractéristique d'un dipôle est la
représentation graphique de la fonction U(I) ou I(U).
Remarques:
-
la
caractéristique dépend de la convention, toujours
la spécifier!
- la valeur I(U=0) est appelée le courant
de court-circuit.
- la valeur U(I=0) est appelée la
tension à vide.
Exemple
d'une photodiode:
4) Les
différents types de dipôles
-
Dipôles symètriques /
non symètriques: si la caractéristique
est impaire alors celui-ci est symétrique (rien ne change
dans un circuit lorsqu'on inverse ses bornes).
-
Dipôles actifs / passifs: si la caractéristique
d'un dipôle passe par l'origine celui-ci est passif, actif
sinon.
-
Dipôles linéaires / non linéaire: si
la caractéristique est une fonction affine le
dipôle est linéaire.
Dans l'exemple
précédent la photodiode est un
dipôle non symètrique, actif et non
linéaire.
-
Dipôles récepteurs /
générateurs: un dipôle
récepteur a une puissance positive et un dipôle
générateur a une puissance négative.
|
Le
signe de la
puissance ne dépend pas de la convention choisie. Un
dipôle recepteur reçoit effectivement une
énergie du circuit, ce qui ne l'empêche pas
d'être parfois étudié en convention
générateur. La puissance, comme
l'intensité et la tension, est une grandeur
algébrique. Par définition on
considère la puissance reçue par un
dipôle et non celle fournie. Ainsi un dipôle
générateur qui fourni effectivement une puissance
au réseau électrique sera
considéré comme possédant une
puissance reçue négative!
|
|
CR |
CG |
| P |
U
I |
-
U I |
| dipôle
récepteur |
P
> 0 |
P
> 0 |
| dipôle
générateur |
P
< 0 |
P
< 0 |
|
Exercice: Bilan de puissance.
5) Les
dipôles linéaires
modèles idéaux:
- La
résistance:
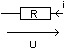 |
CR:
U = R I
I = G U |
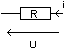 |
CG:
U = - R I
I = - G U |
où
R est la
résistance en Ohms (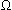 ), et G
est la
conductance en Siemens (S): G = 1 / R . G et R sont définis
positif.
), et G
est la
conductance en Siemens (S): G = 1 / R . G et R sont définis
positif.
 |
Noir: 0
Marron: 1
Rouge: 2
Orange: 3
Jaune:
4
Vert: 5
Bleu: 6
Violet: 7
Gris: 8
Blanc:
9 |

De gauche à droite:
-Premier chiffre
-Deuxième chiffre
-Nombre de zéros
-Précision
Ici R = 5 600 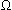 |
 |
Résistances
de puissance maximale d'un 1/4 de W ou 1/2 W.
La bague dorée indique une précision de 5%.
|
- Le
condensateur:
 |
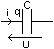 |
i
= C du/dt
q = C u
i = dq/dt |
 |
où
C est la
capacité en Farads (F). Si q est la charge sur l'armature
où arrive le courant (la charge électrique -q est
présente sur l'autre armature) i=dq/dt,
sinon i=-dq/dt . Si q est la charge sur l'armature
où arrive la flêche de la tension alors q=Cu,
sinon q=-Cu . En CG i = - C du/dt .
Par
ailleurs
savoir obtenir
les formes intégrales: i = C du/dt 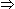 du/dt =
1/C . i du/dt =
1/C . i 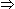 |
 |
(du/dt)dt
= 1/C . |
 |
i
dt  u(t)
= 1/C . u(t)
= 1/C . |
 |
i
dt
+ u(to) . |
- L'inductance:
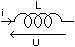 |
u
= L di/dt
L en Henry (H) |
exercice:
établir l'expression
de i(t) sous forme
intégrale. |
- Générateur
de
courant:
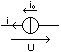 |
Ce
dipôle impose le
courant io dans la branche quelquesoit la tension à ses
bornes:
i=io 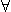 u,
io=cste u,
io=cste |
- Générateur
de tension:
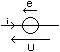
|
Ce
dipôle impose la
tension e à ses bornes quelquesoit le courant dans la
branche:
u=e 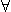 i,
e=cste i,
e=cste |
Exercice: conventions
de signes
6) Dipôles
linéaires réels
Les
dipôles décrit
précédemment sont des idéalisations.
On peut associer plusieurs dipôles modèles pour
approcher la réalité:
| -Bobine
réelle en
Basse Fréquence: |
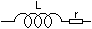
|
-Bobine
réelle en
Haute F: |
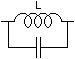 |
|
-
Condensateur avec
résistance de fuite (très grande), en BF:
|
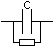 |
-Générateur
de tension de Thévenin
(e: force électromotrice, r: résistance interne): |
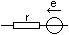 |
-Générateur
de courant de Norton
(io: courant électromoteur, r: résistance
interne): |
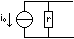 |
Exercices:
générateurs
7)
Association de dipôle linéaires:
a) en
série:
| Raisonnons
tout d'abord sur les résistances: |
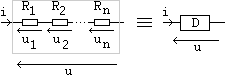
|
d'où:  |
u
= u1
+ u2
+ u3+ ...
i
= i1
= i2 = i3 = ...
uk
= Rk ik
avec k = 1 ... n |
et
finalement nous avons la résistance équivalente:
Réq = R1 + R2 + ... + Rn =  Rk
car u = Réq i
.
Rk
car u = Réq i
.
Exercice:
démontrer que en série
Léq =  Lk
et 1/Céq =
Lk
et 1/Céq =  1/Ck
(pour cette
deuxième relation on dérivera par raport au temps
le relation d'additivité des tensions).
1/Ck
(pour cette
deuxième relation on dérivera par raport au temps
le relation d'additivité des tensions).
b)
en
parallèle:
| Raisonnons
tout d'abord sur les inductances: |
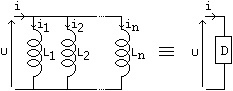 |
d'où:  |
i
=  ik ik
u
= uk
uk
= Lk dik/dt,  k k |
nous
avons: di/dt
=  dik/dt
dik/dt
 di/dt
=
di/dt
=  uk/Lk
=
uk/Lk
=  u/Lk
= [
u/Lk
= [ 1/Lk] . u or u
=
Léq di/dt
d'où: 1/Léq
=
1/Lk] . u or u
=
Léq di/dt
d'où: 1/Léq
=  1/Lk .
1/Lk .
Exercice:
démontrer que en parallèle
Céq =  Ck
et 1/Réq =
Ck
et 1/Réq =  1/Rk .
1/Rk .
On
apprendra par cœur une relation très
utilisée pour deux résistances en
parallèle: Réq =R1R2/(R1+R2)
(à
démontrer).
Exercice:
quelle
est la résistance équivalente pour trois
résistances en parallèle (attention ce n'est pas:
Réq =R1R2R3/(R1+R2+R3), relation non
homogène!)
Exercices: résistances
équivalentes (1).
c)
Des
équivalences utiles:
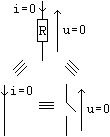
Une résistance pour laquelle on a en
toutes circonstances i=0 (ou u=0) peut être
indifférement remplacée par un fil ou
enlevé du circuit. Si deux points d'un circuit sont au
même potentiel on peut les relier par un fil. Si un fil est
parcouru par un courant nul on peut l'enlever.
(Voir les symètries pour la mise en pratique) |
|
d) symètries:
Dans certains cas l'utilisation des symètrie peut
s'avérer très utile et éviter de
nombreux calculs.
P: plan de symètrie physique du réseau.
Du point de vu électrique P peut être de deux
types:
PS: plan de symètrie pour les
courants et les potentiels.
PAS: plan d'antisymètrie pour les
courants et les potentiels (en prenant le potentiel nul sur le plan).
Une branche placée sur un PAS est
parcourue par un courant nul.
Prenons un exemple (voir figure). Toutes les resistances sont
identiques (R) ce qui
donne naissance à plusieurs symètries: un PS et
un PAS. |
|
Le courant I se sépare en deux
courants identiques j, en effet il n'y a aucunes raisons pour que les
porteurs de charges aillent plus d'un coté que d'un autre.
Même chose quand le courant I ressort.
En appliquant la loi des nœuds
la résistance centrale se trouve parcourue par un courant
nul quelquesoit le courant I ou la tension U imposé
à l'ensemble.
D'après les équivalences vues précedemment nous pouvons donc enlever
cette résistance, et la résistance
équivalente entre les deux bornes est tout simplement R! |
Exercices: résistances
équivalentes (2).
 1,6.10-19
C
(C:
Coulomb), pour un électron q=-e.
1,6.10-19
C
(C:
Coulomb), pour un électron q=-e.

 la
longueur d'onde électromagnétique du
problème
alors pour réaliser l'approximation on doit avoir d
très
petit devant
la
longueur d'onde électromagnétique du
problème
alors pour réaliser l'approximation on doit avoir d
très
petit devant  :
d<<
:
d<<
 =c/f, avec c la vitesse
de la lumière dans le vide et f la
fréquence de l'onde.
=c/f, avec c la vitesse
de la lumière dans le vide et f la
fréquence de l'onde.