.
Nous voulons mesurer
la distance d
entre deux points A et B. Pour cela nous disposons d'un bâton
d'une
longueur d'un mètre. Depuis A jusqu'à B on
reporte le bâton cent fois.
Nous estimons pour chaque report une incertitude de 1 cm.
Quelle est
l'incertitude sur la valeur de d ?
Pour
le savoir nous avons réalisé une simulation
sur Xcas. Nous prenons
un modèle où, pour simplifier, à
chaque report nous tirons à pile ou
face une surestimation de 1 cm ou une sousestimation de 1 cm. Nous
représentons ici les résultats obtenus pour dix
mille mesures de d :
(abscisse:
mesure de d en cm, ordonnée: fréquence de cette
mesure de d)
S> k:=10000;
S>
Evt:=array(1..201,[201]):
S> for r
from 1 to 201 do Evt[r]:=0 od:
S> for j
from 1 to k
> do
> x:=0;
|
> for i from 1
to 100
>
do
>
if rand(2)=0
then x:=x+101
>
else x:=x+99
>
fi:
>
od:
>
Evt[x-9899]:=Evt[x-9899]+1;
|
> od:
S>
coord:=[9900,0],[9900,Evt[1]]:
> for x from 9902 to 10100
> do
> coord:=coord,[x,Evt[x-9900]],[x,Evt[x-9899]]:
> od:
S>
plot([coord],9900..10100); |
Nous avons d=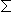 xi
(soit d=x1+x2+...+xi+...+xn),
où les xi sont les
mesures de longueur pour chaque report de bâton.
xi
(soit d=x1+x2+...+xi+...+xn),
où les xi sont les
mesures de longueur pour chaque report de bâton.
 xi est
l'incertitude sur chaque mesure xi. Ici
xi est
l'incertitude sur chaque mesure xi. Ici  xi=1cm et xi=100 +/- 1
cm.
xi=1cm et xi=100 +/- 1
cm.
Quelle est alors l'incertitude  d?
d?
Spontanément nous pourrions penser que  d=
d=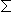
 xi,
d'où ici
xi,
d'où ici  d=100cm
soit 1m pour 100m mesurés de A à B.
d=100cm
soit 1m pour 100m mesurés de A à B.
Mais
problème
ce n'est absolument pas ce qu'indique la simulation! Elle indique
plutôt  d
d
 0,1m.
0,1m.
En effet un simple calcul de probabilités montre qu'il est
extrèmement peu probable d'obtenir, pour d, 99m ou 101m,
alors
que l'on a une chance sur deux, pour xi, d'avoir
0,99m ou 1,01m. Or
nous désirons avoir  d
à probabilité égale de
d
à probabilité égale de  xi.
xi.
En
statistique on utilise la formule
de propagation des incertitudes:
pour une fonction f qui dépend de variables
indépendantes xi, f(x1,x2,...,xi,...,xn), nous
avons:
| ->
|
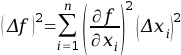 |
<-
|
|
Encore appelée: formule de propagation des erreurs ou des
écarts-types. La formule est exacte pour les
écarts-types, quelquesoit le type de distributions
d'écarts-types finis, dans le cas de variables aléatoires
indépendantes et de petites variations. Pour les incertitudes
elle n'est plus exacte mais c'est une excellente approximation.
Remarque pour les non
initiés
aux dérivées partielles: pour les fonctions
à
plusieurs variables on généralise la notion de
dérivée,
 f/
f/ xi est
la dérivée partielle
de f par rapport à Xi
toutes les autres variables étant
considérées comme des constantes (
xi est
la dérivée partielle
de f par rapport à Xi
toutes les autres variables étant
considérées comme des constantes ( se lit "dé rond"!).
se lit "dé rond"!).
Si f(x,y)=x2-3y+1,  f/
f/ x=2x
et
x=2x
et  f/
f/ y=-3.
y=-3.
Ici  d/
d/ xi=1 et
xi=1 et  xi=
xi= x,
x, 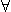 i=1...n, ainsi
i=1...n, ainsi  d=
d= n.
n.  x
soit
x
soit  d=0,1m,
ce qui correspond bien au résultat attendu!
d=0,1m,
ce qui correspond bien au résultat attendu!
Le résultat précédent  d=n.
d=n.  x
était faux et provient de la formule trop souvent
utilisée:
x
était faux et provient de la formule trop souvent
utilisée:
 f=
f=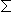 |
| f/
f/ xi|.
xi|.  xi, formule
d'autant plus fausse que le nombre de variables est grand et
les |
xi, formule
d'autant plus fausse que le nombre de variables est grand et
les | f/
f/ xi|.
xi|.  xi de valeurs
proches. Vraie pour des grandeurs non indépendantes, c'est
à dire corrélées.
xi de valeurs
proches. Vraie pour des grandeurs non indépendantes, c'est
à dire corrélées.
Un autre exemple: si d = x1 - x2
alors
 d=
d= (
( x12+
x12+ x22). Si
x22). Si  x1=
x1= x2=1cm avec
90% de confiance alors
x2=1cm avec
90% de confiance alors  d=1,4 cm avec 90%
de confiance. Si nous avions dit
d=1,4 cm avec 90%
de confiance. Si nous avions dit  d=2cm nous
aurions été à 98%
de
confiance (convertisseur de confiances sur la page 1 du programme
IncertitudesLibres, lien à la fin).
d=2cm nous
aurions été à 98%
de
confiance (convertisseur de confiances sur la page 1 du programme
IncertitudesLibres, lien à la fin).
Sur l'indépendance des
variables
aléatoires: un voyageur de commerce part de Paris, va
à
Lyon, puis à Nice et revient pour finir à Lyon.
Celui-ci
indique que la distance Paris-Lyon
est de 465 km et la distance Lyon-Nice
de 479 km. Les distances sont estimées à 10 km
près. Déterminez la distance Paris-Nice puis
celle de
l'aller-retour Lyon-Nice.
Réponses: dParis-Nice= 944 +/-
14 km et daller-retour
Lyon-Nice=
958 +/- 20 km. En effet dans le deuxième cas il n'y a pas
indépendance des variables (c'est la même!), de ce
fait il
ne peut y avoir compensation alèatoire des erreurs, si dLyon-Nice est,
par exemple, surestimée, en multipliant par deux,
l'excés
le sera aussi. Dans le premier cas il peut arriver qu'une distance soit
sous-estimée et l'autre surestimée et il y a
ainsi
possibilité de compensations.
|
|
Pour des
sommes ou des différences les incertitudes absolues au
carré s'ajoutent.
Si f=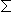 xi alors xi alors  f2= f2=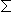  xi2. xi2.
|
|
|
Nous avons
une somme
de carrés de ce fait l'incertitude la plus importante
l'emporte
rapidement. La grandeur la plus incertaine l'emporte sur le
résultat. Si nous ajoutons deux longueurs d'incertitudes 10
cm
et 1 cm, l'incertitude de la somme est de 10,05 cm. La
deuxième
incertitude est ainsi tout à fait négligeable.
Pour des
facteurs le moins précis l'emporte. |
 |
Si nous désirons mesurer une résistance R par la
mesure de U et I: R=U/I alors  R/R=
R/R= ((
(( U/U)2 + (
U/U)2 + ( I/I)2).
Nous choisirons bien sûr le montage courte ou longue
dérivation suivant la valeur attendue de R pour
éviter
une erreur systématique (on ne considère ici que
les
erreurs aléatoires de valeur moyenne nulle).
I/I)2).
Nous choisirons bien sûr le montage courte ou longue
dérivation suivant la valeur attendue de R pour
éviter
une erreur systématique (on ne considère ici que
les
erreurs aléatoires de valeur moyenne nulle).
|
|
Pour des
produits ou des quotients les incertitudes relatives au
carré s'ajoutent.
Si f= xi alors ( xi alors ( f/f)2= f/f)2=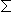 ( ( xi/xi)2. xi/xi)2.
|
|
Fonctionnement de la
calculatrice:
- Pour
R=U/I avec U=25V à 1% et I=12mA à 2%, a=1, a0=1, x0=25,
 x0/x0=1, a1=
-1, x1=0.012
et
x0/x0=1, a1=
-1, x1=0.012
et  x1/x1=2
ce qui donne
R=2083
x1/x1=2
ce qui donne
R=2083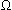 à 2,2%.
à 2,2%.
- Pour
v=
 (2gh), a=1.414, a0=0.5 et a1=0.5 avec disons g=9,8m/s² à
1% et h=50+/-1m, nous prendrons x0=9.8,
dx0/x0=1, x1=50,
(2gh), a=1.414, a0=0.5 et a1=0.5 avec disons g=9,8m/s² à
1% et h=50+/-1m, nous prendrons x0=9.8,
dx0/x0=1, x1=50,  x1/x1=2(%)
et nous obtenons v=31,3 m/s à 1,1%, soit 112,7 +/- 1,3 km/h en
abscence de frottements.
x1/x1=2(%)
et nous obtenons v=31,3 m/s à 1,1%, soit 112,7 +/- 1,3 km/h en
abscence de frottements.
- Pour une mesure de déphasage
 =360°.a/b, avec
a=1,2+/-0,1 et b=9+/-0,1, nous avons
=360°.a/b, avec
a=1,2+/-0,1 et b=9+/-0,1, nous avons  =48° à 8,4 %.
=48° à 8,4 %.
Considérons
l'exemple de la méthode
de Bessel
en focomètrie: on mesure D, distance entre l'objet et
l'image
sur l'écran, et d la distance entre les deux positions de la
lentille (convergente) où l'image est nette. Nous avons
ensuite
la distance focale de la lentille par la relation: f ' = (D2-d2)/4D.
Nous mesurons D=
2000 +/- 10 mm et d= 536 +/- 20 mm. Quelles est alors l'incertitude sur
f'?
 f'/
f'/ D=(D2+d2)/4D2 ,
D=(D2+d2)/4D2 ,
 f'/
f'/ d=-d/2D ,
d=-d/2D ,  f'=
f'= (((D2+d2)/4D2)2 .(
(((D2+d2)/4D2)2 .( D)2
+ (d/2D)2 .(
D)2
+ (d/2D)2 .( d)2) et f'= 463,8 +/- 3,8 mm,
d)2) et f'= 463,8 +/- 3,8 mm,
 f'/f'=0,8%.
f'/f'=0,8%.
Si vous voulez eviter les calculs de dérivées partielles,
en page 4 de IncertitudesLibres, jusqu'à 4 variables, les calculs
sont automatiques (liens en bas de page).
La mesure expérimentale
Précision: justesse, fidèlité et bonne
résolution.
Image des flêches qui visent une cible:
- justesse: l'ensemble des flêches sont
centrées par
rapport au centre de la cible. Si ce n'est pas le cas il y a une erreur
systèmatique, un biais.
- fidèlité: les flêches sont
ressérées, peu de dispersion. La dispersion des
valeurs
est due à l'erreur aléatoire ou accidentelle.
- résolution: d'autant meilleure que la pointe de
la
flêche est petite. Elle est due à la
résolution du
système d'acquisition, c'est l'erreur de
discrètisation.
Etude d'une variable aléatoire
Considérons une variable
aléatoire X, pour chaque mesure nous avons une
réalisation xi
de X. Pour un grand nombre n de mesures nous pouvons tracer la
fréquence fi (nombre de fois que l'on
obtient la même valaur
xi)
en fonction de xi
et nous obtenons généralement une courbe
à profil
Gaussien, courbe en cloche analogue à celle obtenue avec la
simulation sur Xcas. Deux grandeurs définissent cette
distribution : la valeur moyenne xm=(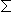 xi)/n
et l'écart-type (correspond à la largeur de la
courbe) s=
xi)/n
et l'écart-type (correspond à la largeur de la
courbe) s= [
[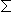 (xi-xm)2/(n-1)].
(xi-xm)2/(n-1)].
Un
cas concret, les fruits d'un arbre sont de tailles diverses, beaucoup
ont une grosseur analogue, certains sont plus gros, d'autre plus
petits. Nous pouvons mesurer une longueur, une masse, une
résistance mécanique, un volume, une couleur ...
les caractéristiques sont innombrables. Un grand nombre de
facteurs aléatoires vont influer sur ces grandeurs:
exposition au Soleil, position dans l'arbre, passage d'un insecte, le
vent, la pluie, le terrain... Mesurons la masse de coings,
nous comptons le nombre de fruits qui appartiennent
à différents intervalles de masse, nous obtenons
une courbes en cloche. Cette courbe est-elle universelle? Oui!!
Un
phénomène résultant d'un grand nombre
de variables aléatoires indépendantes tend vers
une loi gaussienne. L'écart-type est une mesure de cette
variabilité autour de la valeur moyenne.
Enfin
c'est ce que j'ai cru comprendre, pour un grand nombre de mesures, le
théorème centrale limite indique une distribution
de Gauss avec un écart-type s/ n sur la mesure de la
valeur moyenne. n sur la mesure de la
valeur moyenne.
Prenons un
exemple:
Coings
rammassés au sol après une nuit ventée.
|
 |
Pesées en
grammes des 24 coings:
| 92 |
126 |
149 |
196 |
168 |
189 |
| 134 |
106 |
203 |
125 |
106 |
110 |
| 133 |
145 |
156 |
157 |
117 |
125 |
| 72 |
137 |
95 |
120 |
139 |
109 |
Masse
moyenne: 134g
Ecart-type: 33g
|
 |
Pour une courbe de Gauss: 68% des mesures sont
entre xm-s
et xm+s
et 95% entre xm-2s
et xm+2s.
Ainsi si nous effectuons une nouvelle mesure il y a une chance sur 20
quelle soit en dehors de ce dernier intervalle.
La gaussienne correspond à un nombre infini de mesures, pour
un nombre fini il faut apporter une correction: il y a un
élargissement de l'écart type par un facteur t.
Celui-ci tient compte à la fois du nombre de mesures et du
pourcentage.
Vous pouvez obtenir les coefficients t de Student sur un tableur:
=LOI.STUDENT.INVERSE((100-p)/100;n-1)
par exemple.
Page 1 de IncertitudesLibres, lien à la fin.
|
| t |
n=2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
20 |
50 |
infini |
| 90% |
6,31 |
2,92 |
2,35 |
2,13 |
2,02 |
1,94 |
1,89 |
1,86 |
1,83 |
1,73 |
1,68 |
1,64 |
| 95% |
12,7 |
4,30 |
3,18 |
2,78 |
2,57 |
2,45 |
2,36 |
2,31 |
2,26 |
2,09 |
2,01 |
1,96 |
| 99% |
63,6 |
9,92 |
5,84 |
4,60 |
4,03 |
3,71 |
3,50 |
3,36 |
3,25 |
2,86 |
2,68 |
2,58 |
Pour n mesures il y a p% de
chance pour qu'une nouvelle mesure soit entre xm -
tn,p.s et xm
+ tn,p
.s.
Pour n mesures il y a p% de chance pour que la valeur moyenne des
mesures soit entre
xm - tn,p .s /
 n
et xm
+ tn,p .s
/
n
et xm
+ tn,p .s
/  n.
n.
Pour
n=24 et une confiance de 95% nous avons t=2,07 , ainsi 95% des valeurs
sont entre 65g et 202g et la masse moyenne est de
134 +/- 14g.
Pour 90% t=1,71 et si je vais ramasser un nouveau coing il y a 9 chance
sur 10 que sa masse soit entre 78 et 190g.
Nous pourrions maintenant peser l'ensemble des 24 coings, supposons que
nous trouvions une masse de 3209 +/- 1g. La masse moyenne de ces 24 coings est donc de
133,71+/-0,04g. Ce résultat n'est pas en contradiction avec
celui du dessus, 134
+/- 14g c'est
l'incertitude sur la masse moyenne, centre de la courbe de Gauss,
estimée pour l'ensemble des coings produits par l'arbre, et
non pour ces 24 coings en particuliers pésés avec
une balance spécifique.
La
régression linéaire
Pages 2 et 3 de IncertitudesLibres.
Programme
IncertitudesLibres (licence libre et gratuite) : tableur OpenOffice 2.4 .ods
.xls
Licence GNU GPL: https://www.linux-france.org/article/these/gpl.html

 0,1m.
0,1m.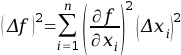

 =360°.a/b, avec
a=1,2+/-0,1 et b=9+/-0,1, nous avons
=360°.a/b, avec
a=1,2+/-0,1 et b=9+/-0,1, nous avons 
